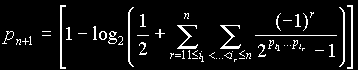analitikus függvénynek, az algebrista számára egy "véges test karakterisztikája vagy egy "nem-arkhimédeszi értékelés", a kombinatorika iránt elkötelezettek a prímeket induktív módon a

pé en plusz egy egyenlő (egy mínusz log kettő (egyketted plusz szumma r = 1től n-ig szumma 1 <= i 1 < ...< i r <= n -1 az r-dik hatványon per kettő a pé el egy től p el r-dikenig mínusz egy))

(itt [x] az x egészét jelöli) rekurzióval [3], míg a logika mûvelôi a

F(a,b,c,d,e,f,g,h,i,j,k,l,m,n,o,p,q,r,s,t,u,v,w,x,y,z)=
(k+2){1-(wz+h+j-q)2-(2n+p+q+z-e)2-(a2 y2 - y2+1 -x2)2 - [(e4+2e3)(a+1)2 + 1 -o2]2 -[16(k+1)3 (k+2) (n+1)2 +1 - f2]2-- [((a+u4 -u2a)2 -1)(n+4dy)2 +1 -(x+cu)2]2-(ai+k+1-l-i)2 - [(gk+2g+k+1)(h+j)+h-z]2-[16r2y4(a2-1)+1-u2]2- [p-m+l(a-n-1)+b(2an+2a-n2 -2n -2)]2 - (n+l+v-y)2 - [z-pm+pla-p2l+t(2ap-p2-1)]2-(a2l2 -l2+1-m2)2 - [q-x+y(a-p-1)+s(2ap+2a-p2 -2p-2)]2}

huszonhat változós polinom pozitív értékeiként definiálhatják [6].

Ismeretes továbbá, hogy a prímszámok a természetes számok építôkövei, azaz minden természetes szám - a tényezôk sorrendjétôl eltekintve - egyértemûen írható fel prímszámok szorzataként.

Három példa kapcsán kövessük nyomon, hogyan merültek föl olyan egyszerû, "klasszikus" kérdések, amelyekre a teljes válasz sokáig hiányzott és amelyekÚjabb, elôre nem látott problémákhoz vezettek. Elôször a prímszámok eloszlásáról szólok, egy problémáról, amelyhez ez elsô részeredmények már Euklidész óta rendelkezésre állnak és amelynek teljes megoldásáért hallhatatlanságot ígértek. Azután a faktorizáció problémájáról beszélek, ahol is egy megadott természetes szám prímtényezôs felbontását kell megadni, s végül a prímszámproblémáról, ahol egy adott n-rôl eldöntendô, hogy vajon prímszám-e. Ez utóbbi probléma a számítógépek használata révén új kérdéseket vetett fel a bizonyítások korrektségét illetôen, míg a faktorizáció problémája mindenek elôtt a kriptográfiai módszerekkel kapcsolatosan vált újra aktuálissá.
visszakezdőlaptovább