Nem mélyedhetünk el most annak részleteiben, hogyan valósultak meg ezek a rendezô elvek a kultúra olyan területein, mint a filozófia, világnézet, zene, irodalom, festészet, csak utalunk e tekintetben Spinóza "Ethica, ordine geometrico demonstrata" címû fômûvében közreadott etikájára.

Nem kívánjuk azonban titkolni azt sem, hogy már a 18. Században fölerôsödtek az ilyen módszerek dominanciája ellen szóló hangok. A "more geometrico" érvelés elleni tiltakozást a mûvészetben egy matematikai klisé irodalmi karrierjén több, mint két évszázadon keresztül követhetjük nyomon. Montecula 1758-ban megjelent matematika- történetében arról számol be, hogy a matematikus Roberval egy szinházi elôadást (Racin: Iphigenia) követôen feltette a kérdést: qu'est-ce que la prouve? Ezt az anekdótát azóta az irodalomban - többszörösen módosítva - újra és újra felhasználták.

Mi lemondunk e "karrier" egyes állomásainak felidézésérôl és teszünk egy ugrást egészen Berthold Brechtig, aki Nietzsche esztétikájához kapcsolódva arra mutatott rá, hogy az egyes diszciplínákban az egymástól eltérô, összhangba nem hozható felfogások élnek a bizonyításról [1]:

"Ha a matematikusunknak egy olyan verset mutattunk volna, amely a Pitagorasz tételt bizonyítja, vajon állította volna-e, hogy az a vers bizonyít valamit? Talán igen, de talán épp mi ellenkeztünk volna vele, mint ahogy tettük ezt akkor is, amikor azt állította, hogy az Ipigenia nem bizonyít semmit." Itt a vita már ahhoz az átfogó kérdéshez vezet, hogy mi a bizonyítás funkciója a "kijelentések igazságát" illetôen. Erre a problematikára késôbb még visszatérünk.

A természetes számokból áradó egyetemes bûvölet után térjünk most át konkrét kérdésekre, amelyek a prímszámok tulajdonságaira vonatkoznak és nem kevésbé tartották igézetükben a tudósok nemzedékeit már a görögök óta.

Mindnyájan tudjuk: Egy prímszám olyan 1-nél nagyobb természetes szám, amely az 1 kivételével semmilyen más, tôle különbözô természetes számmal nem osztható. Ez a számelmélettel foglalkozók definíciója is, de más matematikusok alkalmasint más definíciókat használnak. Így például egy függvénytanban érdekelt számára egy prímszám egész értékû gyöke az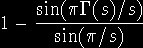