Es ist nicht unser Bestreben, hier an dieser Stelle über die Vielfalt der Forschungsaktivitäten in der AG Zahlentheorie zu berichten – es würde den vorgegebenen Rahmen sprengen, andererseits geben die Schautafeln im Bauteil D 3 einen ausreichenden Überblick. Stattdessen wollen wir einige "Hintergrundinformationen" zu unserer Suche nach großen Primzahlzwillingen geben. Dabei könnte das Motto des Themenkreises lauten: "Auch Mathematiker gehen zuweilen auf Rekordjagd", wie es die Wochenzeitschrift DIE ZEIT am 17.5.1996 in ihrem Bericht über unseren Primzahlzwillingsrekord formuliert hat. Für uns war dieser "sportliche Grund" aber nicht alleine maßgebend.

Primzahlen und Primzahlzwillinge

Allen ist bekannt: Eine Primzahl ist eine natürliche Zahl größer als 1, die durch keine weitere natürliche Zahl außer der 1 geteilt wird. Dies ist auch die Definition der Zahlentheoretiker, andere Mathematiker benutzen ab und zu andere Definitionen. So ist etwa für den Funktionentheoretiker eine Primzahl die ganzzahlige Wurzel der analytischen Funktion

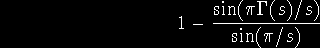
1 - (sin (pi mal gamma (s) / s) / sin (pi / s))

für den Algebraiker ist sie

    "die Charakteristik eines endlichen Körpers"

oder

    "eine nicht-archimedische Bewertung",

der Kombinatoriker definiert die Primzahlen induktiv durch die Rekursion

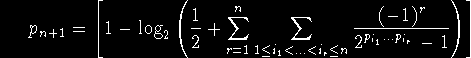
p n+1 = 1 - log 2 (1/2 + summa r = 1 bis n summa 1<= i1 < ... < i r <=n -1 hoch r / 2 hoch (p i 1 ... p i r) - 1)

([x]: ganzzahliger Teil von x)

und der Logiker als die positiven Werte des Polynoms

F(a, b, c, d, e, f, g, h, i, j, k, l, m, n, o, p, q, r, s, t, u, v,w, x, y, z) =

    (k + 2){1 – (wz+ h + j – q)2– (2n + p + q + z –e)2 – (a2y2– y2 + 1 –x2)2– [(e4+ 2e3)(a + 1)2+ 1 – o2]2– [16(k + 1)3(k+ 2)(n + 1)2+ 1 – f2]2– [((a + u4– u2a)2– 1)(n + 4dy)2+ 1 – (x + cu)2]2– (ai + k + 1 – l –i)2 – [(gk+ 2g + k + 1)(h + j)+ h – z]2– [16r2y4(a2– 1) + 1 – u2]2– [p – m + l(a–n–1)+ b(2an + 2a – n2– 2n – 2)]2– (n + l + v – y)2– [z – pm + pla– p2l + t(2ap– p2 – 1)]2– (a2l2– l2 + 1 –m2)2– [q – x + y(a– p – 1) + s(2ap + 2a– p2 – 2p –2)]2}.

Wir begnügen uns mit der erstgenannten Definition.

Über die Verteilung der Primzahlen haben wir bereits seit Euklid erste Informationen: Es gibt unendlich viele Primzahlen.Seine Argumentation gilt bis heute als Paradebeispiel für einen eleganten mathematischen Beweis, den wir alle in der Schule kennengelernt haben und den auch die, für die Mathematik ein Horror war, verstehen konnten. Das genannte Resultat läßt sich auch anders formulieren: Die Primzahlenfunktion (x), die die Anzahl der Primzahlen unterhalb x angibt, strebt gegen für 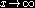. Gauss vermutete bereits als Fünfzehnjähriger (1792), daß

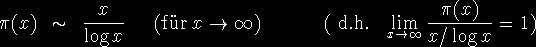
pi x ~ x / log x ( für x -> unendlich ) (d.h. lim x -> unendlich pi x / x / log x = 1)

ist, aber erst 1896 konnte dieses Resultat bewiesen werden. Dieser sogenannte Primzahlsatz läßt sich auch statistisch interpretieren: Die Wahrscheinlichkeit für eine natürliche Zahl der Größenordnung x, eine Primzahl zu sein, ist ungefähr 1 / log x, d.h. in einem Intervall um x der Länge a liegen etwa a / log x Primzahlen (damit dies statistisch sinnvoll ist, sollte a genügend groß, aber klein im Vergleich zu x sein). Entsprechend ist die Wahrscheinlichkeit dafür, daß zwei zufällig (in der Umgebung von x) gewählte Zahlen beide Primzahlen sind, etwa 1/(log x)2. Bezogen auf Primzahlzwillinge, d.h. Paare von Primzahlen, deren Differenz 2 ist, bedeutet dies, daß in Intervallen der genannten Art a/(logx)2 Primzahlzwillinge zu erwarten sind. (In Wirklichkeit etwas mehr, da die Tatsache, daß n prim ist, die Wahrscheinlichkeit für n+2, prim zu sein, verändert (z.B. ist n+2 dann sicher ungerade)). Heuristische Überlegungen führen zu einer Formel

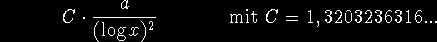
C mal a / (log x) hoch 2 mit C = 1,3203236316

für die Anzahl der Primzahlzwillinge im Intervall [x, x+a]. Numerische Rechnungen führen zu überraschenden Übereinstimmungen mit der Theorie, überraschend insbesondere für Primzahlzwillinge, da noch nicht einmal bekannt ist, ob unendlich viele Primzahlzwillinge existieren.

Intervall Primzahlen Primzahlzwillinge
erwartet gefunden erwartet gefunden
[108, 108+ 150.000] 8142 8154 584 601
[1010, 1010+ 150.000] 7238 7242 461 466
[1011, 1011+ 150.000] 5922 5974 309 276
[1012, 1012+ 150.000] 5429 5433 259 276
[1013, 1013+ 150.000] 5011 5065 221 208
[1014, 1014+ 150.000] 4653 4643 191 186
[1015, 1015+ 150.000] 4343 4251 166 161

Suche nach großen Primzahlzwillingen

In einem Projekt "Massiv parallele Rechner in der Computational Number Theory" entwickelten und implementierten wir Algorithmen für das schnelle Rechnen (z.B. Multiplikation) für sehr große Zahlen mit bis zu einer Milliarde Binärstellen. Bezüglich der erreichten Rechengeschwindigkeit, etwa der Multiplikation, haben wir einige Vergleiche in der folgenden Abbildung angegeben.

Die klassische Schulmethode ist nur für Zahlen mit weniger als einigen hundert Binärstellen optimal (jeweils abhängig von der Hardware). Weit besser ist – bis zu zehntausend Binärstellen – die einfache rekursive Methode von Karatsuba. Für noch größere Zahlen sind komplexere Methoden, die auf der Fast-Fourier-Transformation (FFT) beruhen, den anderen Verfahren überlegen. Eine Möglichkeit ist die Gleitkomma FFT, eine andere die schnelle Multiplikation in Restklassenringen auch die modulo Fermatzahlen. Welche schneller ist, hängt jeweils von der Hardware ab. Zum direkten Vergleich mit den von Schönhage A. (Schönhage et. al. Fast algorithms: a multitape turing machine implementation. BI-Wiss.-Verlag 1994) veröffentlichten Zeiten von 30 µs, 7ms, 3s für die Multiplikationen von 160 bit-, 3200 bit- bzw. 332224 bit-Zahlen sind unsere Zeiten 12 µs, 1.3 ms bzw. 0.46 s, wobei alle Resultate jeweils auf einer SUN S10 40 MHz erzielt wurden.

Die Geschwindigkeit der Multiplikationen ist der "kritische" und ausschlaggebende Teil in vielen Bereichen der "Computational Number Theory" oder auch der numerischen Mathematik. Denn nicht nur die Division kann auf die Multiplikation zurückgeführt werden (indem man die Newton-Approximation zur Berechnung der Reziproken benutzt), sondern auch die Multiplikation von Polynomen, die Berechnung algebraischer und anderer Funktionen und weiterer, darauf basierender Operationen.

So ist die Multiplikation beispielsweise grundlegender Bestandteil unserer Programme für probabilistische Primzahltests und des Primzahltests für Fermatzahlen Fn = 22n+ 1. Die beiden folgenden Diagramme vermitteln einen guten Eindruck von der erreichten Geschwindigkeit, insbesondere gegenüber Supercomputern.

Kehren wir zurück zur eingangs erwähnten Rekordjagd nach großen Primzahlzwillingen. Das zugrundeliegende Such-Prinzip läßt sich kurz wie folgt beschreiben.

  1. Die Suche wurde für die Zahlen in der arithmetischen Progression (5775 + 30030h)260000 ±1 geplant. Hierbei war der Exponent 60000 fest, während sich h zwischen 1 und 227 bewegte.

  2. Aus dieser Folge wurden alle Zahlen herausgesiebt, die einen Faktor zwischen 7 und 241 besitzen. Genau 280.186 Kandidaten überstanden diese Prüfung.

  3. Danach wurden die Kandidaten einem probabilistischen Primzahltest unterzogen, zuerst der –1 Fall, danach der +1 Fall, bis ein "wahrscheinlicher Primzahlzwilling" gefunden wurde. Bereits der 65.000. Kandidat erwies sich als "wahrscheinlicher" Rekordzwilling.

  4. Dieser Zwilling wurde mit exakten Tests (der –1 Fall durch einen Test von Lucas, der +1 Fall durch den Test von Brillhart, Lehmer und Selfridge) überprüft, und dann stand fest: 2.409.110.779.845·260000± 1 sind Primzahlzwillinge.

Literatur

  1. K.-H. Indlekofer, A. Járai, Largest known twin primes, Math. Comp. 65(1996), 427-428. MR 96d:11009
  2. K.-H. Indlekofer, A. Járai, Some world records in computational number theory, Leaflets in Mathematics,  Janus Pannonius University, Pécs,  6(1998), 49-56, ISSN 1416-0935
  3. K.-H. Indlekofer, A. Járai, Largest known twin primes and Sophie Germain primes, Math. Comp. 68(1999), 1317-1324. MR 99k:11013