Multiplikation
Die Multiplikation
ist eine der wichtigsten Routinen unseres für massiv parallele Rechner
entwickelten Programmpakets.
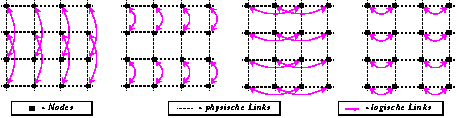
Die Hypercube-Struktur ist ideal für unseren auf der Fouriertransformation
basierenden Multiplikationsalgorithmus.
Wegen ihrer geringen Kommunikationsanforderungen wird die Fermatzahl-Transformation
verwendet. Dabei erfolgen die Teilberechnungen modulo einer Fermatzahl.
Die Multiplikation besteht nach der Zerlegung der Eingabe in digits
aus der Fouriertarnsformation, der digit-by-digit Multiplikation, der inversen
Fouriertransformation und der Normalisation.
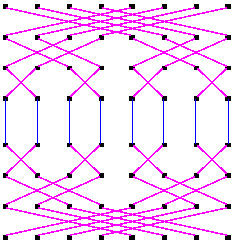
Die Abbildung zeigt den Datenfluß während der
Fouriertransformation, der digit-by-digit Multiplikation und der inversen
Fouriertransformation.
Kommunikation bei der Fouriertransformation
Das Waring'sche Problem
Theoretischer Hintergrund
Im Jahre 1770 behauptete E. Waring, daß man jede natürliche
Zahl als Summe von vier Quadraten, von neun Cuben, von neunzehn Biquadraten,
usw. darstellen kann. Bezeichne
g(k) die kleinste Zahl
n,
so daß sich jede ganze Zahl als Summe von
n ganzen nichtnegativen
Zahlen darstellen läßt, die k-te Potenzen sind. 1772 fand J.
A. Euler eine untere Schranke für
g(k), nämlich
g(k)
>= [ 3
k / 2
k]
+ 2
k - 2. Hilbert zeigte 1909, daß
g(k)
für jedes
k endlich ist. Ein Ergebnis von L. E. Dickson und
Pillai von 1935 ermöglicht, daß man eine strenge Form der Waring'schen
Vermutung
g(k) = [ 3
k / 2
k]
+ 2
k
- 2 mit Hilfe von Rechnern
überprüfen kann.
Resultate
1964 wurde
g(k) = [ 3
k /
2
k] + 2
k
-
2 für
k <= 200.000 auf einen IBM 7090 mit einer Rechenzeit
von 240 Stunden von R. M. Stemmler bewiesen. 1988 hat M. C. Wunderlich
die Vermutung auf einer 65536-Prozessor-Maschine für
k <=
175.000.000 nachgeprüft. 1990 hat Kubina mit Hilfe einer speed-up
Methode von J. R. Deshouillers und J. Selfridge die Vermutung für
alle
k <= 471.000.000 untersucht.
1995 konnten wir auf der massiv parallelen GCel-Architektur mit 1024
Transputern im Paderborn Center for Parallel
Computing - unter Verwendung unserer Multiplikationsroutinen - die
Waring'sche Vermutung für k <= 5.368.709.120 bestätigen.
Die Rechenzeit betrug ca. 4 Stunden.
Resultate aus dem Projekt: "Massive parallele Rechner
in der Computational Number Theory".