|
|
Fraktale und Zahlensysteme
 |
Aktuelle
Wissenschaft und Technik können ohne die Methoden der Zahldarstellung
und ohne effektive arithmetische Operationen mit Zahlen nicht existieren.
Gegenstandsbereiche des Projektes "Fraktale und Zahlensysteme"
sind
- allgemeine, komplexe Zahlensysteme in algebraischen Zahlkörpern
und
- topologische, insbesondere fraktale Eigenschaften der zu diesen Entwicklungen
gehörenden Mengen.
Dabei können einerseits topologische Aussagen (z.B. bezüglich
der Hausdorffdimension) algorithmisch und somit durch Computer bewiesen
werden, andererseits helfen die von Computerprogrammen erzeugten Bilder,
die theoretischen Ergebnisse zu verstehen und Beweisideen zu finden.
|
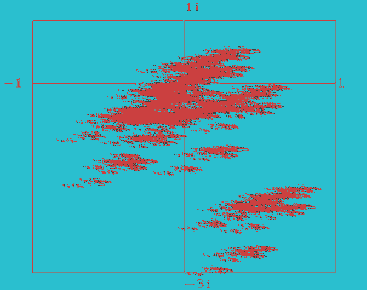
| Abb. oben: Derartige Fraktale sind selbstähnliche Mengen. |
|
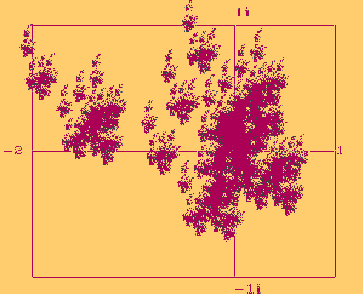
| Abb. rechts: Vergrößerung eines Teils der oberen Mengen.
|
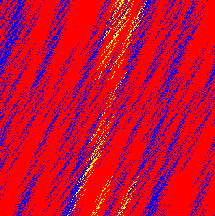
| Abb. unten: Das Finden eines Zahlensystems unter "simultanen Zahlensystemen"
ist keine einfache Aufgabe. |
 |
Mit fraktaler Geometrie und Zahlensystemen beschäftigen wir uns
bereits seit Jahren in einem Kooperationsprojekt mit der Eötvös
Loránd Universität Budapest und der Kossuth Lajos Universität
Debrecen. Diese Forschung wurde überwiegend durch die DFG (Deutsche
Forschungsgemeinschaft) und die MTA (Ungarische Akademie der Wissenschaften)
unterschützt. Im Verlaufe des Projektes ergaben sich neue Einsichten
und mathematische Vermutungen bezüglich der topologischen Strukturen
von Fraktalmengen. |
Literatur
-
K.-H. Indlekofer, I. Kátai
, P. Racsk�, Number systems and fractal geometry, Probability
theory and applications, Math. Appl., 80, Kluwer Acad. Publ., Dordrecht, 1992,
319-334. MR 94g:11089
-
K.-H. Indlekofer, I. Kátai
, P. Racsk�, Some remarks on generalized number systems,
Acta Sci. Math. (Szeged) 57 (1993), no. 1-4, 543-553. MR 94i:11010
-
K.-H. Indlekofer, A.
Járai, I. Kátai
,On some properties of attractors generated by iterated
function systems,
Acta Sci. Math. (Szeged) 60 (1995), no. 1-2, 411-427. MR 96j:11104
|
|