1. Potenzfunktionen   

Die Funktionen 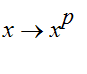         sind
    - streng wachsend auf [0, )  für p>0  (Bild 1: durchgezogene Linien)
   - streng fallend auf      (0, ) für p<0       (Bild 1: gepunktete Linien)
   - konstant auf (0, )  für p=0    


(Bild 1: Potenzfunktionen mit positiver  Basis und beliebigen Exponenten)


Anmerkung:  Für ganzzahlige Exponenten lassen sich die Potenzfunktionen auch
auf (- ,0) bzw. ( ,0] fortsetzen. In diesem Fall  ist die Funktion
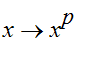
   -  wachsend auf ( ]  für ungerade positive p (d.h., p=2n+1,  )
   -  wachsend auf ( , 0)  für gerade negative p (d.h., p=-2n ,  )
   -  fallend auf  ( ,0] für gerade positive p (d.h., p=2n,  )
    -   fallend auf ( ,0)  für ungerade negative p (d.h., p=-2n+1, )   



(Bild 2: Potenzfunktionen mit ganzzahligen Exponenten)

2. Exponentialfunktionen       

Die Exponentialfunktionen 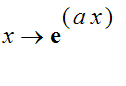      (Bild)


(Bild 3: Exponentialfunktionen)

sind
   - wachsend auf R für  a>0
   - fallend auf R für a<0

4.3. Die (natürliche) Logarithmusfiunktion    

    ist streng wachsend auf (0, ).  
(Im Bild: durchgezogene rote Linie.)



( Bild 4: Logarithmusfunktionen)

Anmerkung:  Wählt man statt der Naturkonstanten e eine andere Zahl  a > 0 als Basis des
Logarithmus, so kennzeichnet man das zunächst durch die Bezeichnung  "  " .
Es gilt also die Beziehung
                          
(im Falle a=2 bzw. a= 10 schreibt man auch kurz ld x bzw. lg x  und nennt dies den
dyadischen  bzw. dekadischen  Logarithmus von x).  
Nun hängt das Monotonieverhalten der Logarithmusfunktion natürlich von der Wahl der
Basis a > 0  ab: sie ist
    - streng wachsend auf (0, )  für a > 1   
   - streng fallend auf (0, )  für a < 1

4.4. Winkelfunktionen  

Die nachfolgende Abbildung zeigt die Graphen der Sinus- und Cosinusfunktion:


Bild: Winkelfunktionen.ps